CDQ+斜率优化
题目描述
小 \(Y\) 最近在一家金券交易所工作。该金券交易所只发行交易两种金券: \(A\) 纪念券(以下简称 \(A\) 券)和 \(B\) 纪念券(以下简称 \(B\) 券)。每个持有金券的顾客都有一个自己的帐户。金券的数目可以是一个实数。每天随着市场的起伏波动,两种金券都有自己当时的价值,即每一单位金券当天可以兑换的人民币数目。我们记录第 \(K\) 天中 \(A\) 券和 \(B\) 券的价值分别为 \(A_K\) 和 \(B_K\)(元/单位金券)。为了方便顾客,金券交易所提供了一种非常方便的交易方式:比例交易法。比例交易法分为两个方面: - 卖出金券:顾客提供一个 \([0,100]\) 内的实数 \(\text{OP}\) 作为卖出比例,其意义为:将 \(\text{OP}\%\) 的 \(A\) 券和 \(\text{OP}\%\) 的 \(B\) 券以当时的价值兑换为人民币; - 买入金券:顾客支付 \(\text{IP}\) 元人民币,交易所将会兑换给用户总价值为 \(\text{IP}\) 的金券,并且,满足提供给顾客的 \(A\) 券和 \(B\) 券的比例在第 \(K\) 天恰好为 \(\text{Rate}_K\) ;例如,假定接下来 \(3\) 天内的 \(A_k , B_k , \text{Rate}_K\) 的变化分别为:

假定在第一天时,用户手中有 \(100\) 元人民币但是没有任何金券。用户可以执行以下的操作:
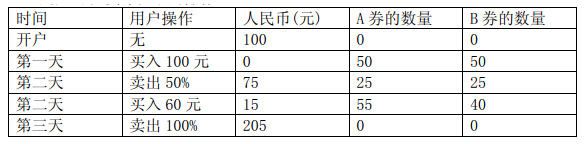
注意到,同一天内可以进行多次操作。小 \(Y\) 是一个很有经济头脑的员工,通过较长时间的运作和行情测算,他已经知道了未来 \(N\) 天内的 \(A\) 券和 \(B\) 券的价值以及 \(\text{Rate}\) 。他还希望能够计算出来,如果开始时拥有 \(S\) 元钱,那么 \(N\) 天后最多能够获得多少元钱。
题解
这是一篇直线型斜率优化的题解
这道题真的很难想...
考虑下面的提示:
在最优方案里,不存在某一时刻,手里既有钱,又有金券。 这启发我们枚举上一次买入的天数: \[f(i)=max\{f(i-1),max_{j=0}^{i-1}\{fa(j)*a(i)+fb(j)*b(i)\}\}\] \[fa(i)=fb(i)*rate(i)\] \[fb(i)=f(i)/(rate(i)*a(i)+b(i))\] 其中\(f(i)\)表示第i天能得到的最多钱数,\(fa(i),fb(i)\)分别表示第i天将手中的钱花光所得到的金券。
直接暴力DP是\(O(n^2)\)的,不能过。考虑只存在i,j乘积项,试试斜率优化。
首先:有两个关于i,j的乘积项,好像不能表示成一条直线的形式?
因为a.b都是常量数组,我们将等式两边都除以b(i),得到: \[f(i)/b(i)=max\{fa(j)*(a[i]/b[i])+fb(j)\}\]
这样,把\(fa\)看做斜率,把\(a/b\)看做x坐标,就是斜率优化的经典柿子辣。然后,我们就可以啊掉这道题了...吗?
容易发现,本题的斜率和坐标都不单调,正常的斜率优化不珂做..
果断弃疗
全都单调的时候单调队列,一个不单调的二分,两个都不单调的时候...CDQ分治!
我们考虑通过排序先消除一维的影响,再通过分治消除另一维。 具体步骤是这样的:
- 分治之前,先将询问按照x坐标(本题中即\(a_i/b_i\))排序。
- 开始分治,设当前区间为[l..r]:(为方便表示,设mid=(l+r)/2);
- 将询问按照时间顺序分成[l..mid]和[mid+1..r]两部分。
- 递归解决[l..mid]的部分。
- 用[l..mid]的DP值去更新[mid+1..r]的DP值。(先构造左半边的凸壳,然后计算右半边的答案,由于我们已经在递归左半边的时候将决策按照fa排序了,而右半边还没有递归,保持\(x\)坐标单调的性质,所以直接按照正常的方法用单调队列插入和删除决策就可以了。(见步骤7))
- 递归解决[mid+1..r]的部分
- 将[l..mid]和[mid+1..r]两个序列按照\(fa(i)\)归并排序。(方便返回上一层递归的时候计算右半边的值)
- l==r的时候我们应该用i-1的决策更新一下i的决策,因为f是要取历史最大值的。顺便计算一下fa.fb的值。
时间复杂度由于采用了归并排序,为\(O(n\lg n)\)。实际速度和平衡树差不多,但是码量把平衡树踩爆啦!
代码: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
using std::sort;
const int maxn=2e5+100;
const double eps=1e-5;
double a[maxn],b[maxn],rate[maxn];
double ans[maxn];
struct Node
{
int id;
double f,fa,fb;
}Q[maxn];
template<class T>inline T max(T a,T b){return a<b?b:a;}
template<class T>inline T min(T a,T b){return a<b?a:b;}
inline void separate(int l,int r)
{
static Node tmp[maxn];
int mid=(l+r)>>1;
for (int i=l,lp=l,rp=mid+1;i<=r;++i)
if (Q[i].id<=mid) tmp[lp++]=Q[i];
else tmp[rp++]=Q[i];
memcpy(Q+l,tmp+l,sizeof(Node)*(r-l+1));
}
inline double K(int x){return Q[x].fa;}
inline double B(int x){return Q[x].fb;}
inline double X(int x){return a[Q[x].id]/b[Q[x].id];}
inline double intersection(int x,int y){return (B(x)-B(y))/(K(y)-K(x));}
inline void solve(int l,int r)
{
int mid=(l+r)>>1;
static int q[maxn];
int head=0,tail=0;
for (int i=l;i<=mid;++i)
{
while (head<tail && intersection(i,q[tail-1])<=intersection(q[tail],q[tail-1])) --tail;
if (K(q[tail])!=K(i)) q[++tail]=i;
}
for (int i=mid+1;i<=r;++i)
{
while (head<tail && K(q[head])*X(i)+B(q[head])<=K(q[head+1])*X(i)+B(q[head+1])) ++head;
Q[i].f=max(Q[i].f,b[Q[i].id]*(K(q[head])*X(i)+B(q[head])));
}
}
/**
** f(i)=max{fa(j)*a(i)+fb(j)*b(i)}
** i.e. f(i)/b(i)=max{fa(j)*(a[i]/b[i])+fb(j)}
** fa(i)=fb(i)*rate(i)
** fb(i)=f(i)/(rate(i)*a(i)+b(i))
**/
inline void CDQ(int l,int r)
{
static Node tmp[maxn];
if (l==r)
{
int idx=Q[l].id;
Q[l].f=max(Q[l].f,ans[idx-1]);
Q[l].fb=Q[l].f/(rate[idx]*a[idx]+b[idx]);
Q[l].fa=Q[l].fb*rate[idx];
ans[Q[l].id]=Q[l].f;
return;
}
int mid=(l+r)>>1;
separate(l,r);
CDQ(l,mid);
solve(l,r);
CDQ(mid+1,r);
for (int lp=l,rp=mid+1,tp=l;tp<=r;++tp)
{
if ((rp>r) || (lp<=mid && Q[lp].fa<=Q[rp].fa))
tmp[tp]=Q[lp++];
else tmp[tp]=Q[rp++];
}
memcpy(Q+l,tmp+l,sizeof(Node)*(r-l+1));
}
int main()
{
int n,s;
scanf("%d%d",&n,&s);
for (int i=1;i<=n;++i)
scanf("%lf%lf%lf",a+i,b+i,rate+i),Q[i].id=i;
ans[0]=s;
sort(Q+1,Q+n+1,[](const Node& x,const Node& y) -> bool {return a[x.id]/b[x.id]<a[y.id]/b[y.id];});
CDQ(1,n);
printf("%.3lf\n",ans[n]);
}